Cho dãy ~A~ gồm ~N~ số nguyên không âm ~a_1, a_2, ..., a_n~. Một bước nhảy từ phần tử ~a_i~ đến phần tử ~a_j~ được gọi là bước nhảy xa nhất của dãy nếu thỏa mãn các điều kiện sau:

• ~1 \leq i < j \leq N~
• ~a_j - a_i \geq P~
• ~j - i~ lớn nhất (Khi đó ~j - i~ được gọi là độ dài bước nhảy xa nhất của dãy).

Yêu cầu

Tìm độ dài bước nhảy xa nhất của dãy ~a~.

Input

Dòng đầu tiên chứa hai số nguyên ~n~ và ~p~ (~1 \leq n \leq 10^5; 0 \leq p \leq 10^9~).

Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, ..., a_n~ (~0 \leq a_i \leq 10^9~ với ~1 \leq i \leq n~).

Output

Một số nguyên dương duy nhất là độ dài của bước nhảy xa nhất của dãy (Nếu không có bước nhảy nào thỏa mãn thì ghi kết quả bằng 0).

Sample Test

Input

6 3
4 3 7 2 6 4

Output

3

Trên trục tọa độ Ox, cho ~N~ điểm khác nhau ~P_1, P_2, ..., P_N~. Đoạn thẳng ~AB~ được gọi là đoạn thẳng chia đều nếu nó được xác định bởi 3 điểm cho trước ~A, B, M~ sao cho ~M~ là trung điểm của ~AB~.

Yêu cầu

Cho biết tọa độ của ~N~ điểm ~P_1, P_2, ..., P_N~. Hỏi có bao nhiêu đoạn thẳng chia đều được tạo ra từ các điểm đã cho?

Input

Dòng 1: ghi số nguyên dương ~N~ (~N \leq 10^3~);

Dòng 2: ghi lần lượt các số thực ~x_1, x_2, ..., x_N~ (~|x_i| \leq 10^5~) tương ứng là tọa độ của các điểm ~P_1, P_2, ..., P_N~.

Output

Một số duy nhất là kết quả tìm được của bài toán.

Sample Test

Input

5
3 -1 2 5 4

Output

3

Cho dãy số ~a~ có ~N~ phần tử nguyên ~a_1, a_2, ..., a_n~ và một số nguyên ~S~ bất kì. Một dãy con liên tiếp của dãy số có dạng ~a_i, a_{i+1}, ..., a_j~ với ~1 \leq i \leq j \leq N~, tổng của dãy con liên tiếp ~a_i, a_{i+1}, ..., a_j~ là ~a_i + a_{i+1} + ... + a_j~, độ dài dãy con liên tiếp ~a_i, a_{i+1}, ..., a_j~ bằng ~j - i + 1~.

Yêu cầu

Tìm dãy con liên tiếp của dãy số ~a~ có độ dài lớn nhất và có tổng không lớn hơn ~S~.

Input

Dòng 1: ghi số nguyên ~N~ và ~S~;

Dòng 2: ghi lần lượt các số nguyên ~a_1, a_2, ..., a_N~ (~|a_i| \leq 10^6, i = 1..N; N \leq 10^3~).

Output

Một số duy nhất là số độ dài dãy con liên tiếp thỏa mãn.

Sample Test

Input

8 7
6 8 -2 4 -5 1 9 3

Output

5

Công ty Omega tổ chức chương trình quay số siêu trúng thưởng cho khách hàng nhân dịp kỷ niệm 100 năm ngày thành lập công ty. Công ty có một bảng điện tử gồm ~n~ ô được đánh số từ ~1~ đến ~n~, mỗi ô hiển thị một số nguyên dương. Người quay số được quay ~m~ lần, mỗi lần quay được một số nguyên dương khi đó trên bảng điện tử các ô có số trùng với số của mỗi lần quay sẽ bị xóa. Sau ~m~ lần quay tiền thưởng của khách hàng là tổng lớn nhất của một loại số trong các số còn hiển thị trên bảng điện tử.

Em hãy đóng vai là người quay số đó và thử vận may của mình nhé.

Yêu cầu

Hãy cho biết các số còn hiển thị trên bảng điện tử và tổng số tiền thưởng của mình là bao nhiêu?

Input

• Dòng 1: ghi số nguyên dương ~n~ và ~m~ (~n, m \leq 3 \times 10^6~);
• Dòng 2: ghi ~n~ số nguyên dương ~A_1, A_2, ..., A_n~ (~A_i \leq 10^9, i = 1..n~) là các số trên bảng điện tử;
• Dòng 3: ghi ~m~ số nguyên dương ~B_1, B_2, ..., B_m~ (~B_j \leq 10^9, j = 1..m~) là các số sau mỗi lần quay.

Output

• Dòng 1: ghi các số còn hiển thị trên bảng điện tử sau ~m~ lần quay theo thứ tự ban đầu;
• Dòng 2: ghi tổng tiền thưởng nhiều nhất có thể được.

Nếu các số trên bảng điện tử bị xóa hết, thì đưa ra số 0.

Sample Test

Input 1

8 5
1 7 5 3 2 5 7 5
3 1 4 6 4

Output 1

7 5 2 5 7 5
15

Input 2

8 5
1 7 5 3 2 5 7 16
3 1 4 6 4

Output 2

7 5 2 5 7 16
16

Cho một dãy số nguyên dương ~a_1, a_2, ..., a_N~ và một số nguyên dương ~S~.

Yêu cầu

Tìm độ dài nhỏ nhất của dãy con chứa các phần tử liên tiếp của dãy mà có tổng các phần tử lớn hơn hoặc bằng ~S~.

Input

Dòng 1 ghi 2 số ~N~ và ~S~ ở dòng đầu. (~10 < N < 10^5~, ~S < 10^7~)

Dòng 2 chứa các phần tử của dãy ~a_1, a_2,...,a_n~ (~a_i \leq 10^4~)

Output

Một số nguyên duy nhất là độ dài của dãy con tìm được.

Sample Test

Input

10 15
5 1 3 5 10 7 4 9 2 8

Output

2

Nhảy lò cò là trò chơi dân gian của Việt Nam, Người trên hành tinh X cũng rất thích trò chơi này và họ đã cải biên trò chơi này như sau: trên mặt phẳng vẽ ~n~ vòng tròn được đánh số từ 1 đến ~n~. Tại vòng tròn ~i~ người ta điền số nguyên dương ~a_i~. hai số trên hai vòng tròn tùy ý không phân biệt nhất thiết phải khác nhau. Tiếp đến người ta vẽ các mũi tên là: nếu có ba số ~a_i, a_j, a_k~ thỏa mãn ~a_k = a_i + a_j~ thì vẽ mũi tên hướng từ vòng tròn ~i~ đến vòng tròn ~k~ và mũi tên hướng từ vòng tròn ~j~ đến vòng tròn ~k~. Người chơi chỉ được di chuyển từ một vòng tròn đến một vòng tròn khác nếu có mũi tên xuất phát từ một trong số các vòng tròn, di chuyển theo cách mũi tên đã vẽ đi đến các vòng tròn khác. Người thắng cuộc sẽ là người tìm được cách di chuyển qua nhiều vòng tròn nhất.

Ví dụ: Với 5 vòng tròn và các số trong vòng tròn là 1, 2, 6, 4, 3, trò chơi được trình bày trong hình dưới đây:

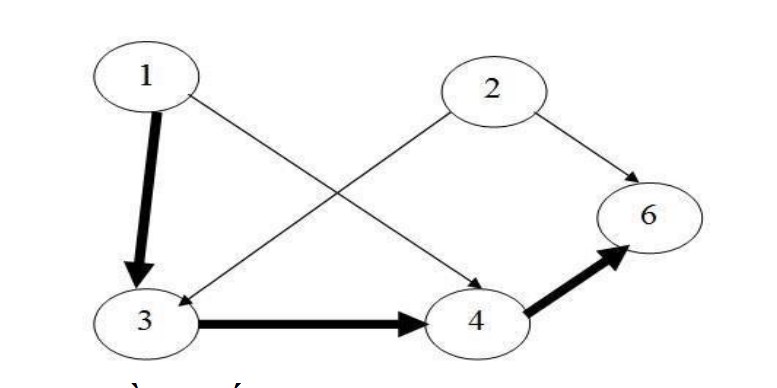
Khi đó có thể di chuyển được nhiều nhất qua 4 vòng tròn (tương ứng với đường đi chuyển được tô đậm trên hình vẽ).

Input

• Dòng đầu chứa số nguyên ~n~ (~3 ≤ n ≤ 1000~);
• Dòng thứ hai chứa dãy số nguyên dương ~a_1, a_2, ... a_n~ (~a_i ≤ 10^9~, ~i = 1, 2, ..., n~). Hai số liên tiếp trên một dòng được ghi cách nhau bởi dấu cách.

Output

• Số lượng vòng tròn trên đường di chuyển tìm được.

Sample Test

Input

5
1 2 6 4 3

Output

4

Ràng buộc

~60\%~ tests ứng với ~60\%~ số điểm của bài có ~3 ≤ n ≤ 100~

Trong khu vườn, người ta trồng một hàng cây chạy dài gồm có ~N~ cây, mỗi cây có độ cao là ~a_1, a_2,...a_n~. Người ta cần lấy ~M~ mét gỗ bằng cách đặt cưa máy sao cho lưỡi cưa ở độ cao ~H~ (mét) để cưa tất cả các cây có độ cao lớn hơn ~H~ (dĩ nhiên những cây có độ cao không lớn hơn ~H~ thì không bị cưa).

Ví dụ: Nếu hàng cây có các cây với độ cao tương ứng là 20, 15, 10 và 18 mét, cưa lấy 7 mét gỗ. Lưỡi cưa đặt tại độ cao hợp lí là 15 mét thì độ cao của các cây còn lại sau khi bị cưa tương ứng là 15, 15, 10 và 15 mét. Tổng số mét gỗ lấy được là 8 mét (dư 1 mét).

Yêu cầu

Hãy tìm vị trí đặt lưỡi cưa hợp lí (số nguyên ~H~ lớn nhất) sao cho lấy được ~M~ mét gỗ và số mét gỗ dư ra là ít nhất.

Input

Dòng đầu chứa số nguyên ~N~ và ~M~ (~1 ≤ N ≤ 10^6~, ~1 ≤ M ≤ 2 \times 10^9~) cách nhau một dấu cách.

Dòng thứ hai chứa ~N~ số nguyên dương ~a_i~ là độ cao của mỗi cây trong hàng (~1 ≤ a_i ≤ 10^9~, ~i = 1, ..., N~), mỗi số cách nhau ít nhất một dấu cách.

Output

Một số nguyên là giá trị cần tìm.

Sample Test

Input

4 7
20 15 10 18

Output

15

Ở đầu ra của một dây chuyền sản xuất trong nhà máy ~ZXY~ có một máy xếp tự động. Sau khi kết thúc việc gia công trên dây chuyền, các sản phẩm sẽ được xếp vào các hộp có cùng dung lượng ~M~. Sản phẩm rời khỏi dây chuyền được xếp vào hộp đang mở (khi bắt đầu ca làm việc có một hộp rỗng được mở sẵn) nếu như dung lượng của hộp còn đủ để chứa sản phẩm. Trong trường hợp ngược lại, máy sẽ tự động đóng nắp hộp hiện tại, cho xuất xưởng rồi mở một hộp rỗng mới để xếp sản phẩm vào. Trong một ca làm việc có ~n~ sản phẩm đánh số từ 1 đến n theo thứ tự mà chúng rời khỏi dây chuyền. Sản phẩm thứ ~i~ có trọng lượng là ~a_i~ , ~i = 1, 2, ..., n~. Ban Giám đốc nhà máy qui định rằng sản phẩm xuất xưởng của mỗi ca làm việc phải được xếp vào trong không quá ~k~ hộp.

Yêu cầu

Hãy giúp người quản đốc của ca làm việc xác định giá trị ~M~ nhỏ nhất sao cho số hộp mà máy tự động cần sử dụng để xếp đầy n sản phẩm xuất xưởng của ca không vượt quá số ~k~ cho trước.

Input

Dòng đầu tiên chứa hai số nguyên ~n~ và ~k~, (~1 ≤ k ≤ n ≤ 10^5~);

Dòng thứ ~i~ trong n dòng tiếp theo chứa số nguyên dương ~a_i~ (~a_i ≤ 30000~), ~i = 1, 2, ..., n~. Các số trên một dòng cách nhau ít nhất một dấu cách.

Output

Một số nguyên duy nhất là dung lượng của hộp.

Sample Test

Input

9 4
1
1
1
3
2
2
1
3
1

Output

5

Trên mặt biển có ~n~ hòn đảo. Có thể xem mặt biển là một mặt phẳng còn các hòn đảo là các điểm nằm tại các tọa độ ~(x_1, y_1)~, ~(x_2, y_2)~, ..., ~(x_n, y_n)~, nghĩa là đảo thứ ~i~ cách gốc tọa độ ~x_i~ mét theo trục hoành, ~y_i~ mét theo trục tung. Ban đầu mỗi hòn đảo là một hình vuông có chiều dài cạnh là 2 mét (tâm hình vuông là tọa độ các hòn đảo). Sau đó mỗi tháng tùy theo lượng phù sa nhiều hay ít mà mỗi hòn đảo được bồi đắp mở rộng cả bốn hướng mỗi hướng thêm 1 mét (phù sa ít) hay 2 mét (phù sa nhiều) để tạo thành hình vuông lớn hơn. Trong một tháng các hòn đảo đều được bồi đắp giống nhau (cùng 1 mét hoặc cùng 2 mét).

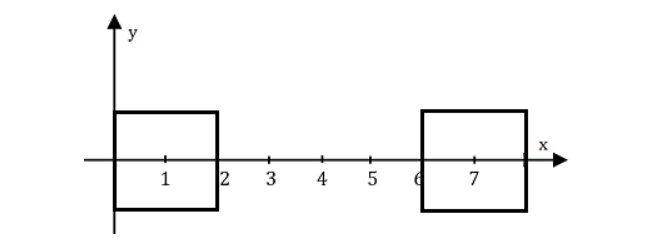
Giả sử nếu quá trình bồi đắp xảy ra trong ~k~ tháng, bạn hãy tính xem có sự va chạm giữa các hòn đảo hay không (ít nhất 2 đảo chạm nhau) và sự va chạm đó xảy ra vào tháng nào. (Nếu sau một tháng nào đó, cạnh hai đảo chỉ mới chạm mép vào nhau, hoặc 2 đỉnh chạm nhau thì cũng xem như tháng đó xảy ra sự va chạm).

Input

• Dòng đầu chứa số nguyên ~T~ là số bộ dữ liệu (~1 ≤ T ≤ 100~).
• Mỗi bộ dữ liệu gồm:
  • Dòng đầu tiên chứa 2 số nguyên ~n~ và ~k~ là số hòn đảo và số tháng bồi đắp, hai số cách nhau một khoảng trắng (~2 ≤ n ≤ 200, 1 ≤ k ≤ 100.000~).
  • Trong ~n~ dòng tiếp theo, tại dòng thứ ~i~ gồm 2 số ~x_i~ và ~y_i~ là tọa độ các hòn đảo, hai số cách nhau một khoảng trắng (~-10^9 ≤ x_i, y_i ≤ 10^9~).
  • Trong dòng tiếp theo là một dãy ~k~ ký tự ứng với ~k~ tháng bồi đắp, nếu đó là ký tự '1' thì tháng đó mở rộng 1 mét, nếu đó là ký tự '2' thì tháng đó mở rộng 2 mét, ngoài ra không có ký tự khác.

Output

• Với mỗi bộ dữ liệu, in ra kết quả trên một dòng:
  • Nếu sau ~k~ tháng không có 2 đảo nào chạm nhau, in ra ~-1~.
  • Nếu có đảo chạm nhau, in ra số nguyên là tháng mà sau khi bồi đắp thì bắt đầu xảy ra va chạm.

Sample Test

Input 1

2 4
1 0
7 0
1122

Output 1

2

Input 2

2 5
1 1
13 13
21112

Output 2

4

Input 3

2 7
1 0
100 1
1121122

Output 3

-1

Một đoạn số có tổng bằng nhau trong một dãy số là một nhóm các số theo đúng thứ tự ban đầu trong dãy mà nếu nhóm với nhau thì sẽ cho ra cùng một giá trị tổng.

Ví dụ với dãy: 2 5 1 3 3 7 thì ta có thể nhóm thành: (2 5) (1 3 3) (7) cùng cho giá trị tổng là 7.

Chú ý: đoạn đặc biệt chứa tất cả các phần tử của dãy cũng được coi là một đoạn có tổng bằng nhau với chính giá trị tổng của số của dãy đó.

Yêu cầu: viết chương trình nhận vào các dãy số nguyên dương và trả về giá trị tổng nhỏ nhất có thể của một đoạn tổng bằng nhau trong dãy.

Input

• Dòng đầu chứa số nguyên ~t~ (~1 ≤ t ≤ 1000~) là số lượng bộ test.
• Tiếp theo là ~t~ bộ test, mỗi bộ test bao gồm:
  • Dòng đầu chứa thứ tự bộ test và số nguyên ~M~ (~1 ≤ M ≤ 10000~) là số phần tử của dãy.
  • Dòng tiếp theo ghi ~M~ số của dãy phân cách bởi 1 dấu cách. (Các số trong dãy đều nhỏ hơn ~20000~).

Output

• Ghi ra cho mỗi bộ test, in ra trên một dòng gồm số thứ tự bộ test và tổng nhỏ nhất có thể đạt được của các đoạn số có tổng bằng nhau.

Sample Test

Input

3
1 6
2 5 1 3 3 7
2 6
1 2 3 4 5 6
3 20
1 1 2 1 1 2 1 1 2 1 1 2 1 1 2 1 1 2 1 1

Output

1 7
2 21
3 2

Sau khi thực thi quy hoạch của Bộ Giao thông, sơ đồ giao thông của thành phố H gồm n tuyến đường ngang và n tuyến đường dọc cắt nhau tạo thành một lưới ô vuông với n x n nút giao thông. Các nút giao thông được gán tọa độ theo hàng từ 1 đến n, từ trên xuống dưới và theo cột từ 1 đến n, từ trái sang phải. Ban chỉ đạo an toàn giao thông quyết định điều động cảnh sát giao thông đến các nút giao thông làm nhiệm vụ. Ban đầu mỗi cảnh sát được phân công đứng trên một nút của một tuyến đường ngang khác nhau. Đến giờ cao điểm, xuất hiện ùn tắc tại các tuyến đường dọc không có cảnh sát giao thông. Để sớm giải quyết tình trạng này, Ban chỉ đạo an toàn giao thông quyết định điều động một số cảnh sát giao thông ở một số nút, từ nút hiện tại sang một nút khác cùng hàng ngang để đảm bảo mỗi tuyến đường dọc đều có mặt của cảnh sát giao thông.

Yêu cầu

Biết rằng cảnh sát ở hàng ngang thứ ~i~ cần ~t_i~ đơn vị thời gian để di chuyển qua 1 cạnh của lưới ô vuông (~i = 1, 2,..., n~), hãy giúp Ban chỉ đạo an toàn giao thông tìm cách điều động các cảnh sát thỏa mãn yêu cầu để đạt ra sao cho việc điều động được hoàn thành tại thời điểm sớm nhất. Giả thiết là các cảnh sát được điều động đồng thời thực hiện việc di chuyển đến vị trí mới tại thời điểm 0.

Input

• Dòng thứ nhất chứa một số nguyên dương n (~n ≤ 10000~).
• Dòng thứ i trong số n dòng tiếp theo chứa hai số nguyên dương ~c_i, t_i~ (~t_i ≤ 10000~) tương ứng là tọa độ cột và thời gian để di chuyển qua 1 cạnh của lưới ô vuông của cảnh sát đứng trên tuyến đường ngang thứ i (~i = 1, 2,..., n~). Hai số trên cùng một dòng được ghi cách nhau ít nhất một dấu cách.

Output

Một số nguyên duy nhất là thời điểm sớm nhất tìm được.

Sample Test

Input

5
5 10
3 10
3 20
2 9
2 15

Output

10

Ràng buộc

~50\%~ số tests ứng với ~50\%~ số điểm của bài có ~n ≤ 100~