Cho số nguyên dương ~n~ và dãy số nguyên ~a_1, a_2, \dots, a_n~. Hãy tìm dãy số ~B~ sao cho ~b_i = a_1 + a_2 + \dots + a_i~, hay nói cách khác ~b_i~ là tổng của ~i~ số đầu tiên trong dãy ~A~.

Input

• Dòng đầu tiên ghi số nguyên dương ~n~ (~1 \leq n \leq 10^6~).
• Dòng tiếp theo ghi lần lượt các số ~a_1, a_2, \dots, a_n~ (~|a_i| \leq 10^9~).

Output

Ghi lần lượt các số ~b_1, b_2, \dots, b_n~.

Sample Test

Input

4
1 4 3 2

Output

1 5 8 10

Hàng năm Trường THPT Chuyên Lê Quý Đôn tổ chức thi Tin học đồng đội, mỗi đội gồm 3 người. Để khuyến khích phong trào học Tin, nhà trường quyết định mỗi đội dự thi phải có một nam và hai nữ. Có ~a~ bạn nữ và ~b~ bạn nam đạt kết quả tốt ở vòng loại chọn thành lập đội tuyển. Do thời gian tổ chức thi của trường trùng với kỳ tin học trẻ của Tỉnh đoàn nên nhà trường quyết định cử ~c~ học sinh trong số những người đã vượt qua vòng loại đi tham gia thi. Những học sinh này sẽ không tham gia vào kỳ thi Tin học sắp tới của trường. Tổ Tin sẽ quyết định danh sách các học sinh dự thi tin học trẻ. Các học sinh đã vượt qua vòng loại đều có thành tích xuất sắc tương đương nhau vì vậy Tổ quyết định sẽ chọn học sinh đi thi sao cho các thí sinh còn lại có thể thành lập được nhiều đội tuyển dự thi nhất.

Ví dụ, với ~a = 6~, ~b = 3~ và ~c = 2~ cần chọn một nam và một nữ đi thi, khi đó phần còn lại sẽ lập được ~2~ đội tuyển (một bạn nữ sẽ không được tham gia thi đồng đội).

Yêu cầu

Cho ~a,b~ và ~c~ (~0 ≤ a,b ≤ 10^{12}; 0 ≤ c ≤ a + b~). Hãy xác định số đội tuyển nhiều nhất có thể thành lập.

Input

Một dòng duy nhất gồm ba số nguyên ~a,b,c~

Output

Một số nguyên duy nhất là số đội tuyển nhiều nhất có thể thành lập

Sample Test

Input

6 3 2

Output

2

Ràng buộc

• ~30\%~ số test ứng với ~30\%~ số điểm có ~0 ≤ a,b ≤ 1000; 0 ≤ c ≤ a + b~.

• ~70\%~ số test còn lại không có ràng buộc gì thêm.

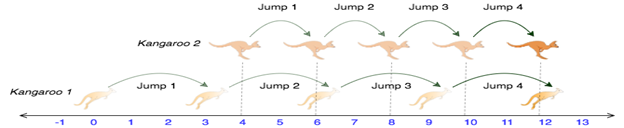
Một trong những tiết mục các bạn nhỏ rất yêu thích trong lần đi dã ngoại ở sở thú là cuộc đua của các chú Kangaroo. Có hai con đang đứng trên một đường thẳng và sẵn sàng nhảy theo hướng dương về phía trước (tức là về phía dương vô cực).

• Con đầu tiên bắt đầu tại địa điểm ~x_1~ và di chuyển với tốc độ ~v_1~ mét mỗi bước nhảy.
• Con thứ hai bắt đầu tại địa điểm ~x_2~ và di chuyển với tốc độ ~v_2~ mét mỗi bước nhảy.

Yêu cầu

Hãy tìm xem sau bao nhiêu bước nhảy để cả hai con Kangaroo ở cùng một vị trí trong cùng một thời điểm sau khi xuất phát, nếu không được thì in ra ~-1~.

Input

Một dòng chứa 4 số nguyên tương ứng với các giá trị ~x_1,v_1,x_2,v_2~ (~1≤x_1<x_2≤10000; 1≤v_1≤10000; 1≤v_2≤10000~)</p>

Output

Một số nguyên duy nhất là số bước nhảy nếu 2 con có thể gặp nhau, ngược lại ghi ~-1~

Sample Test

Input

0 3 4 2

Output

4

Giải thích

2 con Kangaroo sau 4 bước nhảy sẽ gặp nhau ở vị trí 12.

Cho một số nguyên dương ~N~. Ta kí hiệu ~[a_1, a_2, ..., a_M]~ là bội chung nhỏ nhất của ~a_1, a_2, ..., a_M~.

Yêu cầu

Tìm chữ số tận cùng khác 0 của giá trị ~[1, 2, ..., N]~.

Input

Gồm một số dòng, mỗi dòng gồm một số nguyên dương ~N~ (~N \leq 10^6~)

Output

Với mỗi dòng, in ra kết quả tương ứng với ~N~.

Sample Test

Input

6
5
4

Output

6
6
2

Giải thích

• Với ~N = 6~ thì ~[1,2,3,4,5,6] = 60~ nên chữ số tận cùng khác 0 là ~6~.
• Với ~N = 4~ thì ~[1,2,3,4] = 12~ nên chữ số tận cùng khác 0 là ~2~.

Ràng buộc

• ~60\%~ số test ứng với 60% số điểm có ~N ≤ 50~
• ~40\%~ số test ứng với 40% số điểm còn lại không giới hạn gì thêm

Một làng quê có ~m~ chàng trai đánh số từ 1 tới ~m~ và ~n~ cô gái đánh số từ 1 tới ~n~. Chàng trai thứ ~i~ có chiều cao ~a_i~ (~i = 1,2, ..., m~), cô gái thứ ~j~ có chiều cao ~b_j~ (~j = 1,2, ..., n~). Trong một buổi khiêu vũ, người ta muốn chọn ra một số cặp nhảy. Mỗi cặp nhảy gồm đúng 1 chàng trai và 1 cô gái và trong cặp đó, chàng trai phải cao hơn cô gái. Mỗi chàng trai, cô gái trong làng không được tham gia quá 1 cặp nhảy.

Yêu cầu

Tìm một số nhiều nhất các cặp nhảy thỏa mãn yêu cầu trên.

Input

Dòng 1 chứa hai số nguyên dương ~m, n \leq 10^5~

Dòng 2 chứa ~m~ số nguyên dương ~a_1, a_2, ..., a_m~ (Với ~a_i \leq 10^9~)

Dòng 3 chứa ~n~ số nguyên dương ~b_1, b_2, ..., b_n~ (Với ~b_j \leq 10^9~)

Output

Một số nguyên duy nhất là số cặp nhảy theo phương án tìm được.

Sample Test

Input

3 2
1 2 3
2 3

Output

1

Input

4 5
1 2 3 4
2 2 1 4 5

Output

3

Ràng buộc

~50\%~ số điểm ứng với các test có ~m, n \leq 1000~