Hàng năm Trường THPT Chuyên Lê Quý Đôn tổ chức thi Tin học đồng đội, mỗi đội gồm 3 người. Để khuyến khích phong trào học Tin, nhà trường quyết định mỗi đội dự thi phải có một nam và hai nữ. Có ~a~ bạn nữ và ~b~ bạn nam đạt kết quả tốt ở vòng loại chọn thành lập đội tuyển. Do thời gian tổ chức thi của trường trùng với kỳ tin học trẻ của Tỉnh đoàn nên nhà trường quyết định cử ~c~ học sinh trong số những người đã vượt qua vòng loại đi tham gia thi. Những học sinh này sẽ không tham gia vào kỳ thi Tin học sắp tới của trường. Tổ Tin sẽ quyết định danh sách các học sinh dự thi tin học trẻ. Các học sinh đã vượt qua vòng loại đều có thành tích xuất sắc tương đương nhau vì vậy Tổ quyết định sẽ chọn học sinh đi thi sao cho các thí sinh còn lại có thể thành lập được nhiều đội tuyển dự thi nhất.

Ví dụ, với ~a = 6~, ~b = 3~ và ~c = 2~ cần chọn một nam và một nữ đi thi, khi đó phần còn lại sẽ lập được ~2~ đội tuyển (một bạn nữ sẽ không được tham gia thi đồng đội).

Yêu cầu

Cho ~a,b~ và ~c~ (~0 ≤ a,b ≤ 10^{12}; 0 ≤ c ≤ a + b~). Hãy xác định số đội tuyển nhiều nhất có thể thành lập.

Input

Một dòng duy nhất gồm ba số nguyên ~a,b,c~

Output

Một số nguyên duy nhất là số đội tuyển nhiều nhất có thể thành lập

Sample Test

Input

6 3 2

Output

2

Ràng buộc

• ~30\%~ số test ứng với ~30\%~ số điểm có ~0 ≤ a,b ≤ 1000; 0 ≤ c ≤ a + b~.

• ~70\%~ số test còn lại không có ràng buộc gì thêm.

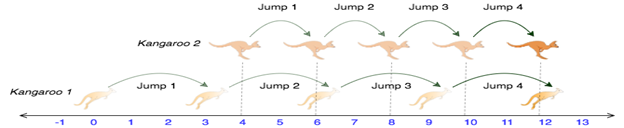
Một trong những tiết mục các bạn nhỏ rất yêu thích trong lần đi dã ngoại ở sở thú là cuộc đua của các chú Kangaroo. Có hai con đang đứng trên một đường thẳng và sẵn sàng nhảy theo hướng dương về phía trước (tức là về phía dương vô cực).

• Con đầu tiên bắt đầu tại địa điểm ~x_1~ và di chuyển với tốc độ ~v_1~ mét mỗi bước nhảy.
• Con thứ hai bắt đầu tại địa điểm ~x_2~ và di chuyển với tốc độ ~v_2~ mét mỗi bước nhảy.

Yêu cầu

Hãy tìm xem sau bao nhiêu bước nhảy để cả hai con Kangaroo ở cùng một vị trí trong cùng một thời điểm sau khi xuất phát, nếu không được thì in ra ~-1~.

Input

Một dòng chứa 4 số nguyên tương ứng với các giá trị ~x_1,v_1,x_2,v_2~ (~1≤x_1<x_2≤10000; 1≤v_1≤10000; 1≤v_2≤10000~)</p>

Output

Một số nguyên duy nhất là số bước nhảy nếu 2 con có thể gặp nhau, ngược lại ghi ~-1~

Sample Test

Input

0 3 4 2

Output

4

Giải thích

2 con Kangaroo sau 4 bước nhảy sẽ gặp nhau ở vị trí 12.

Cho một số nguyên dương ~N~. Ta kí hiệu ~[a_1, a_2, ..., a_M]~ là bội chung nhỏ nhất của ~a_1, a_2, ..., a_M~.

Yêu cầu

Tìm chữ số tận cùng khác 0 của giá trị ~[1, 2, ..., N]~.

Input

Gồm một số dòng, mỗi dòng gồm một số nguyên dương ~N~ (~N \leq 10^6~)

Output

Với mỗi dòng, in ra kết quả tương ứng với ~N~.

Sample Test

Input

6
5
4

Output

6
6
2

Giải thích

• Với ~N = 6~ thì ~[1,2,3,4,5,6] = 60~ nên chữ số tận cùng khác 0 là ~6~.
• Với ~N = 4~ thì ~[1,2,3,4] = 12~ nên chữ số tận cùng khác 0 là ~2~.

Ràng buộc

• ~60\%~ số test ứng với 60% số điểm có ~N ≤ 50~
• ~40\%~ số test ứng với 40% số điểm còn lại không giới hạn gì thêm

Sau kỳ thi, nhà trường giao cho thầy X chuẩn bị phần thưởng để trao cho các học sinh đạt thành tích cao. Giải thưởng được đặt trong những chiếc hộp có kích thước khác nhau. Thầy giáo X có nhiệm vụ chuẩn bị các hộp quà như thế. Thầy có ~N~ hộp quà, các hộp quà được đánh số từ 1 tới ~n~, mỗi hộp quà có kích thước được biểu diễn bằng một số nguyên ~a_i~. Thầy có thể lồng hộp quà thứ ~i~ vào hộp quà thứ ~j~ nếu như hộp quà thứ ~i~ đang rỗng và ~a_i + k ≤ a_j~ với ~k~ là một số nguyên dương cho trước. Bằng cách lồng các hộp quà vào nhau theo cách như vậy, thầy giáo sẽ chỉ cần tìm chỗ để vừa chiếc hộp ngoài cùng (là chiếc hộp không nằm trong bất kì cái hộp nào khác) vì phòng của thầy rất nhỏ.

Yêu cầu

Hãy giúp thầy giáo lồng các hộp quà vào nhau sao cho tổng kích thước các hộp ngoài cùng là nhỏ nhất?

Input

Dòng đầu chứa hai số nguyên dương ~n~ và ~k~ (~n ≤ 10^5; k ≤ 10^9~) cách nhau một khoảng trắng.

Dòng thứ hai chứa ~n~ số nguyên dương ~a_1, a_2, ..., a_n~ (~a_i ≤ 10^9~), mỗi số cách nhau một khoảng trắng thể hiện kích thước hộp quà.

Output

Một số nguyên duy nhất là tổng kích thước các hộp ngoài cùng theo phương án tìm được.

Sample Test

Input

8 2
8 4 2 1 1 3 5 9

Output

18

Sau khi chuẩn bị xong các phần quà, thầy X đã quyết định khóa cửa phòng bằng một ổ khóa số. Mã khóa để mở cửa sẽ gồm 3 chữ số. Thầy giao cho 1 bạn lớp 10 Tin một con số may mắn ~S~ gồm ~N~ chữ số. Thầy quyết định sẽ xóa ~N - 3~ chữ số khỏi ~S~ và nối 3 chữ số còn lại mà không thay đổi thứ tự, dùng để đặt mã mở khóa.

Yêu cầu

Hãy giúp bạn học sinh lớp Tin đếm xem thầy X có thể đặt bao nhiêu mã khóa khác nhau theo cách này?

Ghi chú: Cả số may mắn và mật mã đều có thể bắt đầu bằng số 0.

Input

Dòng đầu tiên là số ~N~ - độ dài của chữ số may mắn (~4 \le N \le 30000~; ~S~ là 1 số có độ dài ~N~, chỉ chứa ký tự số).

Dòng tiếp theo là số may mắn ~S~.

Output

Số cách thầy X tạo ra các mã khóa khác nhau.

Sample Test

Input

4
0224

Output

3

Giải thích

• Xóa số thứ nhất của ~S~ ta được: ~224~;
• Xóa số thứ ~2~: ~024~;
• Xóa số thứ ~3~: ~024~;
• Xóa số thứ ~4~: ~022~.
• Vì thế thầy có thể đặt được ~3~ mã khóa khác nhau là: ~022; 024; 224~.

Ràng buộc

• Có ~50\%~ số test có ~N \le 100~.

Nam biết rằng trong mùa mưa lũ thì khả năng mất điện thường xuyên là rất lớn. Vì vậy anh ấy muốn mua ~M~ cục pin dự phòng cho mùa học đội tuyển. Có ~N~ cửa hàng bán các cục pin dự phòng. Ở cửa hàng thứ ~i~, anh ta có thể mua nhiều nhất ~B_i~ pin dự phòng với giá ~A_i~ đồng mỗi cục.

Yêu cầu

Hãy tính số tiền tối thiểu mà Nam có thể mua được ~M~ cục pin dự phòng. Đảm bảo rằng luôn có một số tiền đủ lớn để có thể mua được ~M~ cục pin.

Input

Dòng đầu tiên chứa 2 số nguyên ~N~ và ~M~ – tương ứng với số cửa hàng và số cục pin dự phòng Nam muốn mua.

~N~ dòng tiếp theo, dòng thứ ~i~ chứa giá trị ~A_i~ và ~B_i~ tương ứng với giá trị của mỗi cục pin.

Output

Số tiền tối thiểu mà Nam có thể mua ~M~ cục pin dự phòng.

Ràng buộc

• ~1 \leq N, M \leq 10^5~; ~1 \leq A_i \leq 10^9~; ~1 \leq B_i \leq 10^5~; ~B_1 + \cdots + B_N \geq M~
• Tất cả các giá trị trong đầu vào là số nguyên, các số cách nhau 1 khoảng trắng.

Sample Test

Input

2 5
4 9
2 4

Output

12

Giải thích

Với ~12~ đồng, Nam có thể mua ~1~ cục pin ở cửa hàng đầu tiên và ~4~ cục pin ở cửa hàng thứ hai, tổng cộng là ~5~ cục pin.

Có ~N~ mặt hàng trong một cửa hàng. Với mỗi ~i = 1,2, ..., N~, giá của mặt hàng thứ ~i~ là ~A_i~ VNĐ (đơn vị tiền tệ của Việt Nam). Nam hiện đang có ~K~ phiếu giảm giá. Mỗi phiếu giảm giá có thể được sử dụng trên một mặt hàng. Nam có thể sử dụng bất kỳ số lượng phiếu giảm giá nào, cũng có thể không, trên cùng một mặt hàng. Sử dụng ~K~ phiếu giảm giá cho một mặt hàng có giá ~a~ đồng cho phép Nam mua nó với giá ~max\{a - K * X, 0\}~ VNĐ.

Yêu cầu

In ra số tiền tối thiểu mà Nam cần để mua tất cả các mặt hàng.

Input

Dòng đầu tiên chứa 3 số ~N, K~ và ~X~.

Dòng thứ 2 chứa ~N~ số nguyên ~A_i~ là giá các mặt hàng tương ứng.

Output

Một số nguyên theo yêu cầu bài toán.

Ràng buộc

• ~1 \leq N \leq 2 \times 10^5~
• ~1 \leq K, X \leq 10^9~
• ~1 \leq A_i \leq 10^9~
• Các giá trị đầu vào là số nguyên.

Sample Test

Input

5 4 7
8 3 10 5 13

Output

12

Giải thích

Bằng cách sử dụng ~1~ phiếu giảm giá cho mặt hàng thứ nhất, ~1~ phiếu giảm giá cho mặt hàng thứ 3 và ~2~ phiếu giảm giá cho mặt hàng thứ 5, Nam có thể:

• Mua món hàng thứ nhất với giá ~max(A_1-X,0)~ là ~1~ đồng;
• Mua món hàng thứ hai với giá ~max(A_2,0)~ là ~3~ đồng;
• Mua món hàng thứ 3 với giá ~max(A_3-X,0)~ là ~3~ đồng;
• Mua món hàng thứ 4 với giá ~max(A_4,0)~ là ~5~ đồng;
• Mua món hàng thứ 5 với giá ~max(A_5 – 2*X,0)~ là ~0~ đồng.

Tổng số tiền nhỏ nhất cần là: ~1 + 3 + 3 + 5 + 0 = 12~.

Trong thời gian tiến hành Đại hội thể dục thể thao, mỗi học sinh được nhận một số hiệu là một số tự nhiên. Cần sắp danh sách các học sinh tham gia Đại hội theo điểm thi đấu của họ.

Yêu cầu

Đưa ra danh sách giảm dần theo thứ tự điểm thi đấu. Nếu hai học sinh cùng số điểm thì sắp tăng theo mã số.

Input

Dòng đầu tiên là số ~N~ - số học sinh (~N \leq 100000~).

~N~ dòng tiếp theo, mỗi dòng gồm ~a_i~ là mã số và ~b_i~ là điểm thi đấu của học sinh thứ ~i~ (~a_i, b_i \leq 10^5~)

Output

Đưa ra danh sách giảm dần theo thứ tự điểm thi đấu. Nếu hai học sinh cùng số điểm thì sắp tăng theo mã số.

Sample Test

Input 1

3
101 80
305 90
200 14

Output 1

305 90
101 80
200 14

Input 2

3
20 80
30 90
25 90

Output 2

25 90
30 90
20 80

Các nhà thám hiểm được tập hợp trong cuộc thám hiểm đến miền Bắc cực. Họ có một chiếc bè lớn gồm ~N \times M~ chiếc bè nhỏ gắn với nhau. Mỗi chiếc bè nhỏ có một sức chứa riêng, và mỗi nhà thám hiểm cũng có trọng lượng của mình. Mỗi chiếc bè nhỏ không thể chở hơn một nhà thám hiểm. Nếu sức chứa của chiếc bè nhỏ hơn trọng lượng nhà thám hiểm chọn nó thì nhà thám hiểm đó có thể bị chết đuối khi bước xuống chiếc bè nhỏ này. Người lãnh đạo cuộc thám hiểm nghĩ cách xếp bè. Hãy giúp đỡ ông ta xác định số nhiều nhất các nhà thám hiểm có thể đi.

Yêu cầu

Xác định số nhiều nhất các nhà thám hiểm có thể tham gia cuộc thám hiểm này.

Input

Dòng đầu tiên là các số ~N~ và ~M~ (~1 \leq N, M \leq 40~).

~N~ dòng tiếp theo, mỗi dòng gồm ~M~ số là sức chứa ~M~ bè nhỏ.

Dòng thứ ~N+2~ là số ~K~ (~1 \leq K \leq 2000~) là số lượng các nhà thám hiểm.

Trong dòng thứ ~N+3~ chứa ~K~ số, số thứ ~i~ trong chúng là trọng lượng nhà thám hiểm thứ ~i~.

Tất cả trọng lượng các nhà thám hiểm và sức chứa các bè không vượt quá ~10^9~.

Output

Một số là số nhiều nhất các nhà thám hiểm tham gia cuộc thám hiểm này.

Sample Test

Input

3 2
5 10
7 5
5 5
6
9 5 3 5 12 10

Output

4

Một làng quê có ~m~ chàng trai đánh số từ 1 tới ~m~ và ~n~ cô gái đánh số từ 1 tới ~n~. Chàng trai thứ ~i~ có chiều cao ~a_i~ (~i = 1,2, ..., m~), cô gái thứ ~j~ có chiều cao ~b_j~ (~j = 1,2, ..., n~). Trong một buổi khiêu vũ, người ta muốn chọn ra một số cặp nhảy. Mỗi cặp nhảy gồm đúng 1 chàng trai và 1 cô gái và trong cặp đó, chàng trai phải cao hơn cô gái. Mỗi chàng trai, cô gái trong làng không được tham gia quá 1 cặp nhảy.

Yêu cầu

Tìm một số nhiều nhất các cặp nhảy thỏa mãn yêu cầu trên.

Input

Dòng 1 chứa hai số nguyên dương ~m, n \leq 10^5~

Dòng 2 chứa ~m~ số nguyên dương ~a_1, a_2, ..., a_m~ (Với ~a_i \leq 10^9~)

Dòng 3 chứa ~n~ số nguyên dương ~b_1, b_2, ..., b_n~ (Với ~b_j \leq 10^9~)

Output

Một số nguyên duy nhất là số cặp nhảy theo phương án tìm được.

Sample Test

Input

3 2
1 2 3
2 3

Output

1

Input

4 5
1 2 3 4
2 2 1 4 5

Output

3

Ràng buộc

~50\%~ số điểm ứng với các test có ~m, n \leq 1000~