Nhảy lò cò là trò chơi dân gian của Việt Nam. Người trên hành tinh X cũng rất thích trò chơi này và họ đã cải biến trò chơi này như sau: trên mặt phẳng vẽ ~n~ vòng tròn được đánh số từ ~1~ đến ~n~. Tại vòng tròn ~i~ người ta điền số nguyên dương ~a_i~: hai số trên hai vòng tròn tùy ý không phân biệt nhất thiết phải khác nhau. Tiếp đến người ta vẽ các mũi tên là: nếu có ba số ~a_i, a_j, a_k~ thỏa mãn ~a_k = a_i + a_j~ thì vẽ mũi tên hướng từ vòng tròn ~i~ đến vòng tròn ~k~ và mũi tên hướng từ vòng tròn ~j~ đến vòng tròn ~k~. Người chơi chỉ được di chuyển từ một vòng tròn đến một vòng tròn khác nếu có mũi tên xuất phát từ một trong số các vòng tròn, di chuyển theo cách mũi tên đã vẽ để đi đến các vòng tròn khác. Người thắng cuộc sẽ là người tìm được cách di chuyển qua nhiều vòng tròn nhất.

Ví dụ: Với ~5~ vòng tròn và các số trong vòng tròn là ~1, 2, 6, 4, 3~, trò chơi được trình bày trong hình dưới đây:

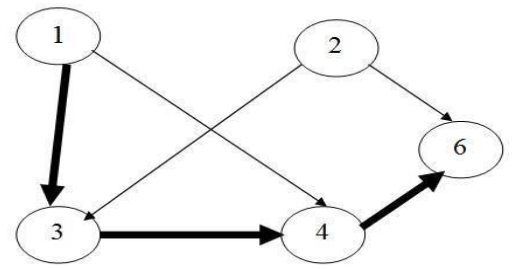
Khi đó có thể di chuyển được nhiều nhất qua ~4~ vòng tròn (tương ứng với đường di chuyển được tô đậm trên hình vẽ).

Yêu cầu: Hãy xác định xem trong trò chơi mô tả ở trên nhiều nhất có thể di chuyển qua bao nhiêu vòng tròn?

Input

Dòng đầu chứa số nguyên n (~3 ≤ n ≤ 1000~).
Dòng thứ hai chứa dãy số nguyên dương ~a_1, a_2, \ldots, a_n~ (~a_i \le 10^9~, với ~i = 1 \ldots n~). Hai số liên tiếp trên một dòng được ghi cách nhau bởi dấu cách.

Output

Ghi ra một số nguyên là số lượng vòng tròn lớn nhất tìm được.

Sample Test

Input

5
1 2 6 4 3

Output

4

Ràng buộc

~60\%~ tests ứng với ~60\%~ số điểm của bài có ~3 ≤ n ≤ 100~.